Solving “Disjoint Set Test” on DMOJ

Problem

Problem link: https://dmoj.ca/problem/ds2

Problem type: Graph theory

This problem asks us to implement a program that outputs the number of edges in the minimum spanning tree of a weighted, undirected graph. Though we are not given the weights of each edge, we are given that “an edge that shows up earlier in the input has a strictly less weight than an edge that shows up later in the input”. If there is no minimum spanning tree (i.e. the graph is not connected) we output “Disconnected Graph”.

Terminology

Node/vertex: an element in a graph

Edge: the connection between two nodes/vertices in a graph

Weight: the “cost” of travelling along an edge in a graph

Directed graph: a graph has that direction; every edge start from one nodes and goes to another

Solution

Disjoint-set

We will need to use the disjoint-set data structure to find the minimum spanning tree of the given graph. What is a disjoint-set data structure? It is a data structure that is used to store a collection of elements that are part of non-overlapping sets, with each set having a representative element.

A disjoint-set (with path compression optimization) has two main operations. The data structure can also be stored in an array, where the value with index i in the array represents i’s parent element’s index.

• Find
  • Returns the representative of a vertex’s set, and sets all vertices in between (including the vertex passed to the function) to be direct children of the representative
• Merge
  • Merges two sets (adds an edge between the representative of the sets of the vertices given)

1
2
3
4
5
6
7
8
9

int find(vertex v) {
    if ds[v] != v:
        ds[v] = find(ds[v])
    return ds[v]
}

void merge(vertex v, vertex u) {
    ds[find(v)] = find(u)
}

Below is an example of how the disjoint-set data structure works.

Assume we have 10 elements to begin with, and all elements are part of their own set. Each set’s representative is the sole element in that set.

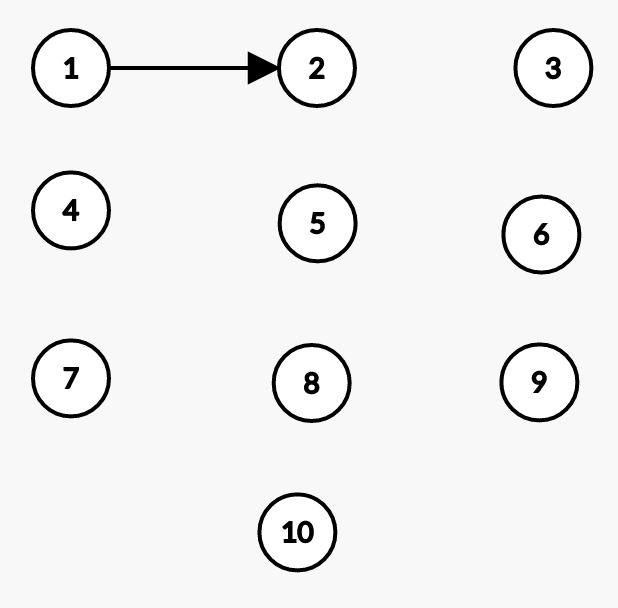
Let’s merge 1 and 2. An edge is added between 1 and 2. merge(1, 2)

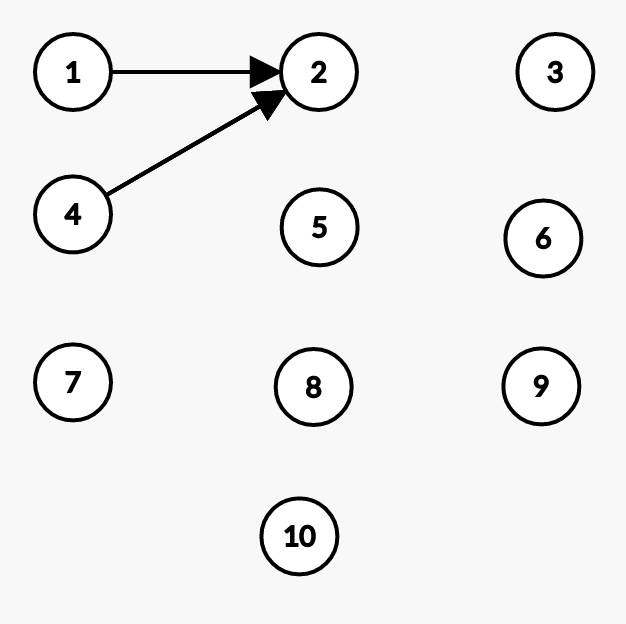
Let’s now merge 4 and 1. An edge is added between 4 and 1’s representative, which is 2.

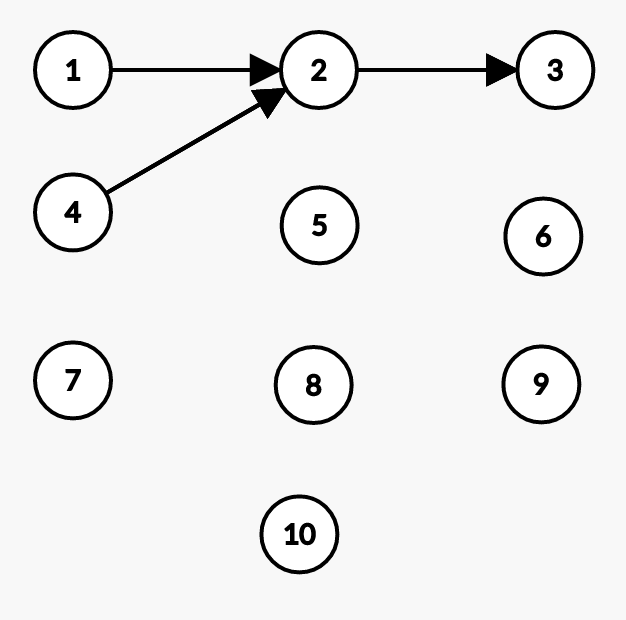
Now, let’s merge 2 and 3. An edge is added between each vertex’s representative.

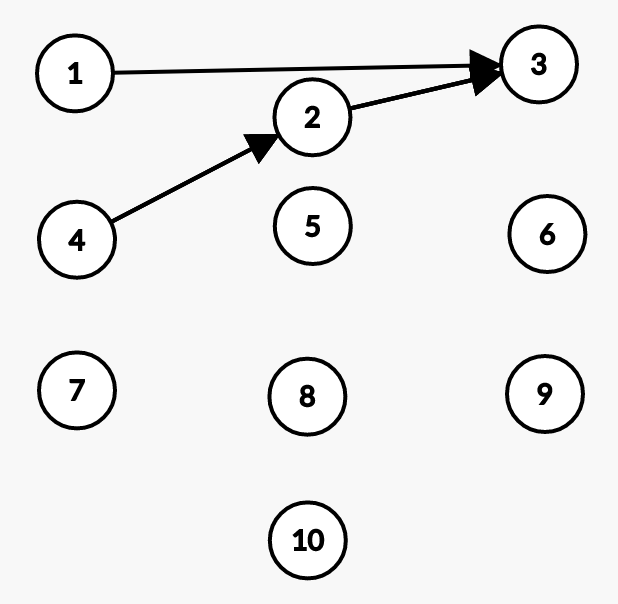
If we were to call find(1) now (finding 1’s representative), it would return 3, and it would also make 1’s direct parent 3. This is known as the path compression optimization.

You might be wondering how the disjoint-set data structure relates to finding the minimum spanning tree of a graph. Finding the minimum spanning tree of a graph can be achieved by using either Prim’s or Kruskal’s algorithm. We’ll be using Kruskal’s algorithm for this problem.

Minimum spanning tree

What is a minimum spanning tree? A minimum spanning tree, in a connected, undirected, weighted graph, is the series of edges that connect the entire graph, while using minimum total edge weight (sum of all weights of the edges visited by the MST).

Below is an example of a minimum spanning tree of a graph.

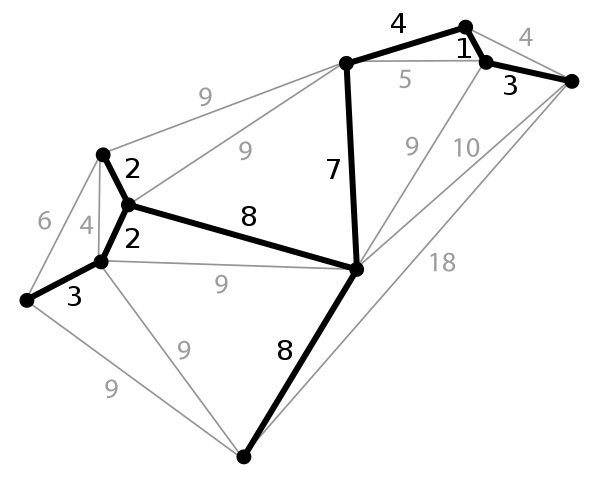
The idea of Kruskal’s algorithm is to sort each edge in non-decreasing order by its weight (which is conveniently how the edges are given in the input), then add the current edge to the minimum spanning tree if the two vertices are not part of the same set. If we have added the current edge, then merge the sets of both of the vertices that are a part of the edge. Kruskal’s algorithm is an example of a greedy algorithm.

If a minimum spanning tree does not exist (if the graph is disconnected), we should output Disconnected Graph. We can check for a connected graph by determining if each element in the disjoint-set has the same representative element after Kruskal’s algorithm has been run. If there exists an element in the disjoint-set such that its representative is not equal to another element’s representative, then the graph is disconnected.

Let’s now test our strategy on the sample inputs.

Sample Case 1

Input

1
2
3
4
5

4 4
1 2
1 3
2 3
3 4

Output

1
2
3

1
2
4

The graph can be represented as follows:

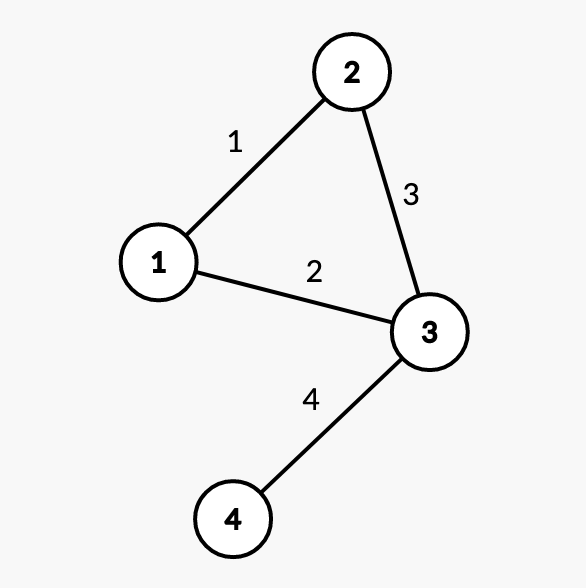
Since we can assume that any edge that comes before another edge in the input has a lesser weight than the edge that comes later, there is no need to sort the input. We will use an array to represent our disjoint-set.

Disjoint-set:

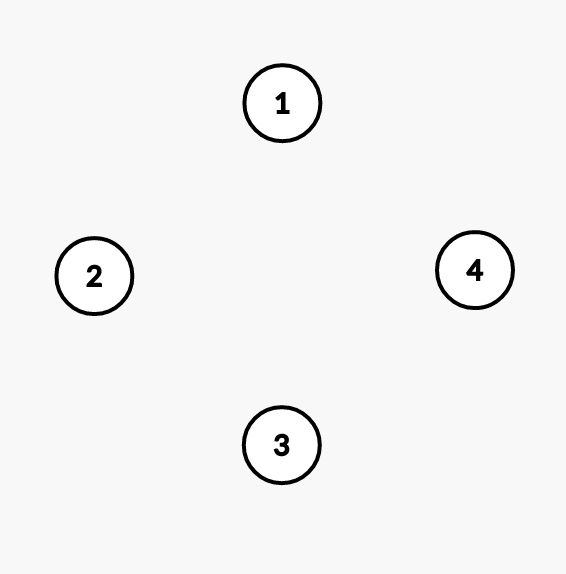
Array (index 0 will not be used):

Minimum spanning tree: {}

Step 1

Edge: 1 2.

Check if 1 and 2 are part of the same set. They are not, so we can merge them. merge(1, 2)

Disjoint-set:

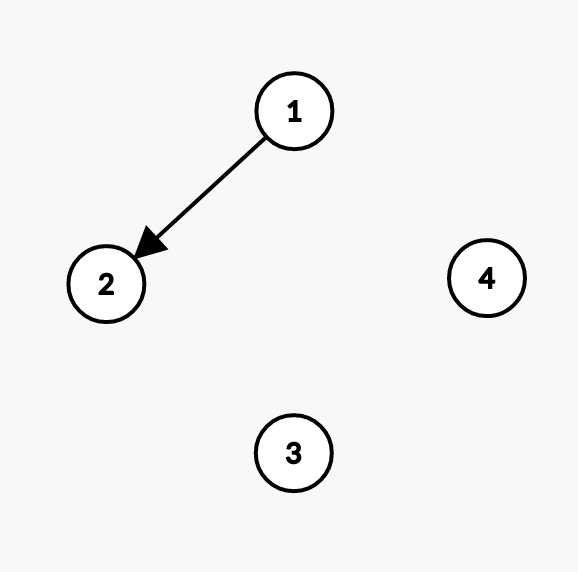
Array:

Minimum spanning tree: {edge 1}

Step 2

Edge: 1 3.

Check if 1 and 3 are part of the same set. They are not, so we can merge them. merge(1, 3)

Disjoint-set:

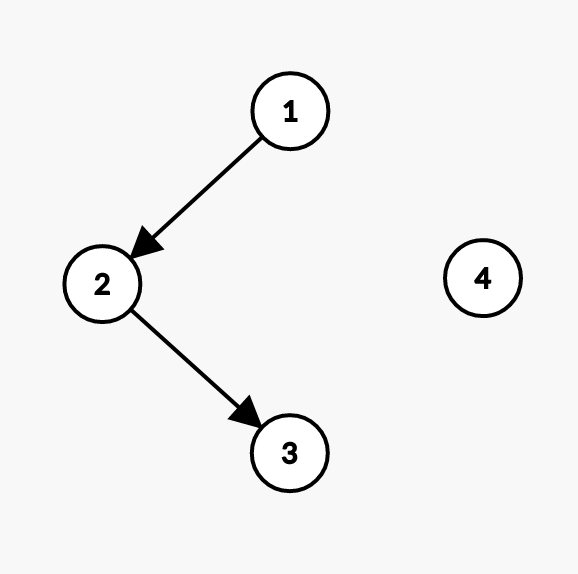
Array:

Minimum spanning tree: {edge 1, edge 2}

Step 3

Edge: 2 3.

Check if 2 and 3 are part of the same set. They are, so do not add the current edge to the minimum spanning tree.

Disjoint-set:

Array:

Minimum spanning tree: {edge 1, edge 2}

Step 4

Edge: 2 4.

Check if 2 and 4 are part of the same set. They are not, so we can merge them. merge(2, 4)

Disjoint-set:

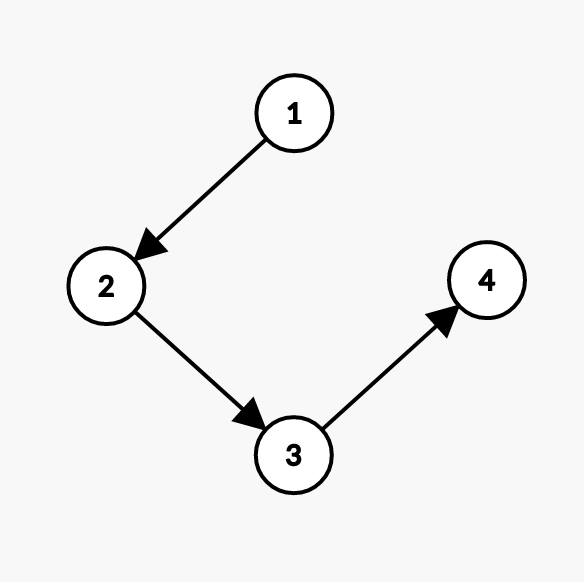
Array:

Minimum spanning tree: {edge 1, edge 2, edge 4}

We realize that each element is a part of the same set and has the same representative (4). We can then output the minimum spanning tree.

Now that we have devised a strategy and have confirmed it with the sample input, we can write the code for this problem.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

#include <bits/stdc++.h>

#define el "\n"

using namespace std;

const int MM = 100001;

int n, m, dsu[MM];
vector<int> mst;
set<int> uni;


int find(int e) {
    if (e != dsu[e]) {
        dsu[e] = find(dsu[e]);
    }
    return dsu[e];
}


void merge(int u, int v) {
    dsu[find(u)] = find(v);
}


int main() {

    cin.tie(0);ios::sync_with_stdio(0);
    
    cin >> n >> m;

    for (int i = 1; i <= n; i++) dsu[i] = i;


    for (int i = 1; i <= m; i++) {
        int u, v;
        cin >> u >> v;
        if (find(u) != find(v)) {
            mst.emplace_back(i);
            merge(u, v);
        }
    }

    for (int i = 1; i <= n; i++) uni.emplace(find(i));

    if (uni.size() > 1) {
        cout << "Disconnected Graph" << el;
        return 0;
    }

    for (auto e : mst) {
        cout << e << el;
    }

    return 0;
}